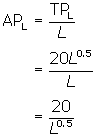3.5 Production
[3.2 Demand]
[3.3
Price Elasticity]
[3.4 Supply]
[3.6 Costs]
Suppose that researchers at Groveji, a company that produces a variety of agricultural
products, have developed a new organic fertiliser that increases crop yield. Groveji decides to handle the production of the organic
fertiliser at a new manufacturing facility.
Like any other firm that produces a
good or a service (outputs),
Groveji requires inputs
such as land, labour (L), and capital
(K). Note that in economics, capital
refers to the machines, equipment and other resources (other than land and
labour) that a firm employs to produce goods and services. This differs from
the financial definition of capital, which refers to shareholders' equity and
retained earnings.
For Groveji,
capital includes the new building, the equipment needed to mix ingredients and
to package the fertiliser, forklifts to transport the finished goods to a
warehouse, and delivery trucks.
When Groveji
managers think about how much output (bags of fertiliser) the company will
produce with its inputs, they immediately think about costs of production. How
much will it cost to produce 3,000 bags per day? What about 5,000 or 10,000
bags per day?
The production costs will vary based on
how much output Groveji produces. How those costs vary will depend on the
production technology used and the costs of Groveji's
inputs. In order to make the best production decisions, the managers turn their
thoughts to production functions.
A production function shows the maximum
level of output a firm can produce using a given level of inputs. A production
function may include one, two or n
inputs. This subject will focus primarily on the two-input case because it is
concise and because its analysis provides all of the economic intuition that
would come from studying production functions with more than two inputs.
Suppose that Groveji
requires two inputs—capital (K) and
labour (L)—to produce the organic
fertiliser. You can show that output (q)
is a function of K and L, by writing it mathematically as
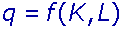
In this production function, q is the number of bags of fertiliser Groveji produces per day; K and L represent the
amount of capital and labour used in production.
Before moving from this general
production function to a more specific production function, you should have
some understanding of production in the short run and production in the long
run. Economists use these concepts to account for the fact that firms are able
to vary the quantity of some inputs more easily than they can vary the quantity
of other inputs.
Production in the Short Run
The
short run
refers to any period of time during which the firm is unable to vary the amount
of at least one input that it uses in production. Inputs with quantities that
cannot be varied in the short run are called "fixed inputs". Inputs
that the firm can vary in the short run are called "variable inputs".
Production in the Long Run The
long run
refers to the time period during which the firm can change the level of any
input that it uses. In other words, all inputs are variable in the long run.
The
distinction between the short run and the long run is a conceptual tool that
economists use to study how a firm's decisions are influenced by the
variability of its inputs.
If
the firm is better able to become profitable when all inputs are variable, what
economists call the long run, then that firm might decide to lease office space
rather than buy it, hire temporary workers instead of permanent employees, and
outsource any activities that might be capital intensive.
For
instance, a firm would not want to build a factory that could produce more
inputs than it was ever likely to sell. By outsourcing, the firm can increase
production quickly if the product becomes popular. More flexible inputs often
tend to be more expensive for a firm, so the firm must compare potential
benefits with costs.
The
following link shows why it is necessary to make a distinction between the
short run and the long run.
The
link here
contains advanced information, which includes some examples of common production
functions
Total Product of Labour
To
see how production functions work, let’s assume that Groveji's
long-run production function looks like this:
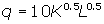
In this function, A = 10, a = 0.5, and b = 0.5.
This function contains exponents. To
review exponents, click on here.
Also assume that at some point in the past, Groveji
decided to purchase four "units" of capital, which is fixed in the
short run. If capital is the fixed input in the short run, and labour is the
variable input, then Groveji's short-run production
function—also called the total product of labour function—is
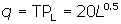
The
total product of labour function shows that when capital is fixed, output
changes as the number of workers changes.
A graph of the total product of labour function will make
this concept clearer. The following animation illustrates this concept.
Average Product of Labour
You
can now also find the average product of labour, APL, which measures
output per unit of labour. Knowing the average product of labour may help a
manager decide whether or not to hire extra workers; it tells the manager
whether output will rise or fall in proportion to the
extra labour. Mathematically, the average product of labour is the ratio of a
firm's output to the number of workers the firm uses to produce that output.

To find average product of labour,
divide the TPL function by L.
Continuing with the example from above, you find
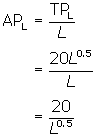
Marginal Product of Labour
The
marginal product of labour, MPL, is the change in output that is
generated by a change in labour. It indicates the number of units of output
produced per additional unit of labour used. Firms consider marginal product of
labour when they decide whether or not to hire additional workers. If a
worker's wage is higher than the value of his marginal output, then it doesn't
make sense for the company to hire him.
One
method of calculating the marginal product of labour is to consider it over a
range of labour.

The symbol D indicates
"change in". You should use this method when changes in labour are
relatively large, such as when a firm hires several additional full-time
employees instead of asking current employees to work some overtime.
This method is also appropriate when the TPL is
not differentiable. For instance, you may have a table that describes the
relation between labour and output, but not a functional form to describe that
relation.
The link here contains advanced material, which explains
how to use calculus to find the marginal product of labour.
Graphically,
the marginal product of labour is the slope
of the total product of labour curve. It indicates the rate of change in output as labour input changes. It answers the
question, How much will output change
when a firm hires one additional unit of labour, holding capital constant?
The
graph below shows average and marginal product of labour.

Diminishing
marginal returns
The
graph of marginal product of labour above shows that each additional worker
increases output but the increase gets smaller and smaller as the firm employs
additional units of labour. This reflects a phenomenon in economics known as
the law of diminishing marginal returns.
The
law of diminishing marginal returns states that additional units of a variable
input eventually result in smaller and smaller increases in output as more of
that variable input is used, holding constant the quantities of the other
inputs (such as capital).
What
is the difference between diminishing returns and diminishing marginal returns?
Click here to find out.
The marginal product of labour
decreases as the amount of labour used increases, holding capital fixed. As a
firm hires more and more workers, each additional worker contributes less to
production. This is consistent with the graph above, where MPL is
downward sloping.
Consider an example. A manufacturing
firm that employs 100 workers may increase its output by hiring an additional
worker. That worker can help other workers or use equipment that previously was
not utilised. Now suppose the firm continues to hire additional workers.
Eventually, adding more and more workers will be of less value than the first
few hires. These additional workers may actually get in the way of other
workers, thereby hindering production. It is important to note that in this
example, capital is fixed. The firm cannot build new factories in which to
employ additional workers.
The following link shows an example of
how to find total, average and marginal cost.

You have just seen how you might
analyse the impact to a firm of changing the quantity of one input it uses. A
firm may also want to consider changing several or all of its inputs. For
instance, suppose a firm wants to increase its output by 10 percent. To do so,
it will need to increase the amount of at least some of its inputs, but by how
much? What would happen if it were to use 10 percent more of all of its inputs? The answer to that
question depends on the firm's production function.
Economists categorise production functions based upon how a
firm's output changes when the firm changes all of its inputs by a certain
percentage. Note that since the firm is changing all inputs, the categories are
relevant only in the long run.
Constant returns to scale
If a firm doubles the amount of all of its inputs, and
output doubles as a result, then the production function exhibits constant
returns to scale. That is, if a proportional increase in all inputs leads to
the same proportional increase in output, the firm will have constant returns
to scale. A straightforward way to express constant returns to scale is with
the following equation:
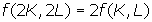
This
equation shows that the firm's output from using 2K units of capital and 2L
units of labour is exactly double the output the firm gets from using K units of capital and L units of labour.
Increasing
returns to scale
If
a firm more than doubles its output by doubling all of its inputs, the firm is
said to have increasing returns to scale. The firm is essentially becoming more
productive with its inputs as it uses more of them. The following inequality
describes increasing returns to scale:
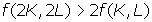
One interpretation of this condition is that two identical
small firms would produce more output if they were to combine their resources
and become one large firm. A single large firm may allow for greater
specialisation of labour or opportunities for dedicating capital for a
particular operation. Mergers can be attractive when firms have production
functions that satisfy this condition.
Decreasing
returns to scale
When
a firm less than doubles its output by doubling all of its inputs, the firm is
said to exhibit decreasing returns to scale. The following inequality describes
decreasing returns to scale:
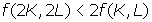
Here, two identical small firms would produce more output
as separate entities than they would if they were to merge into one large firm.
For advanced material on how to express returns of scale
mathematically, continue on.
(Advanced) Expressing Returns to Scale Mathematically
Returns to scale and
Cobb-Douglas
Recall that the general expression of a Cobb-Douglas production function is
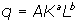
To determine whether this has constant,
increasing or decreasing returns to scale for particular values of A, a and b, you need to compare the output produced when inputs (K, L) are doubled, given by

with twice
the output produced when the original input levels are used, given by

To simplify the comparison, distribute
the exponents in the first expression and collect terms to find

Notice
the similarity between this final expression and the expression for twice the
original output. That is, compare
 with
with 
·
If a
+ b = 1, these two expressions
are equivalent. In this case, doubling inputs exactly doubles the output, so a + b
= 1 yields constant returns to scale
with this general Cobb-Douglas production function.
·
If a
+ b > 1, then
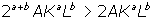
because
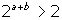
Therefore, if a + b > 1, doubling
inputs more than doubles output. In other words, the production function
exhibits increasing returns to scale.
·
If a
+ b < 1, then
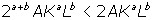
because
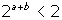
Therefore, if a + b < 1, doubling inputs less than doubles output. The
production function exhibits decreasing returns to scale.
Topic Summary
In this topic, you have learnt how to
·
explain short- and long-run
productivity by identifying the inputs that are difficult to change in the
short run
·
identify the short- and
long-run total, marginal and average product of labour
·
characterise whether a production technology involves increasing or decreasing
returns to scale in the long run.
Now go
on to topic 3.6, “Costs”.
![]()